記事が見づらいなどの問題がありましたらContactからお知らせください。
FXデータ分析の練習(2)〜1変量データの統計量(基礎)〜
投稿日:2019年11月21日
pandasはデータ分析に非常に便利なライブラリです。この記事のシリーズではpandasを使ってFXのデータを分析する練習をしてみました。
はじめに
このPartについて
この記事では前回取得して読み込んだデータを使って1変量の統計量について勉強してみます。ライブラリにメソッドが用意されている計算についても、今回はあくまで勉強なので計算できるところは手で計算してから、そのメソッドを使っています。
ライブラリのimport
import numpy as np
import scipy as sp1変量データの取得
前回のPartでpandasのDataFrameで読み込んだデータから"open"の値を1変量データとして取り出してこのデータについて統計量をみてみます。
data_open = data_concated["open"]平均・代表値
平均(average)はそのデータ全体を表す値でいくつかの種類があり、おもなものとして算術平均(arithmetic mean)、中央値(median)、最頻値(mode)などがあります。
平均は適切な値を選ぶことでそのデータの全体像を表す代表となる数値のため、代表値とも言います。
算術平均(aithmetic mean)
単純に平均といったときにはこの算術平均(arithmetic mean)をさすことが多いでしょう。全ての値の和を値の個数で割った値です。
FXでは平均足や平均値推移の計算の仲で算術平均が使われています。連続データの分析ではいろんなところで使われる指標のようですね。
N = len(data_open)
sum_value = sp.sum(data_open)
arithmetic_mean = sum_value / N
print(arithmetic_mean)1.1553863670015938この値はpandasのDataFrameやnumpyではmean()という関数で取得できます。
print(data_open.mean())
print(np.mean(data_open))1.1553863670015938
1.1553863670015938中央値(median)
中央値(median)はデータを小さい順に並べた時真ん中に来る値です。この値は住民の所得調査などでよく使われます。
例:
ある100人の村で年収の調査をした。住民の99人の年収は300万だが、ある1人の年収は500億円である。この時算術平均によるとこの村の平均年収は5927万円で、中央値の300万円になる。
村の住人の年収はだいたいいくらか?と聞かれて、たった一人の年収に引っ張られる算術平均を使うのはこの場合あまりよくないだろう。
このように中央値を使うことで外れ値の影響をなくすことができます。FXの様なデータの場合外れ値自体が存在しない(もちろん値の取り間違いやDBの操作ミスなどの人的ミスでは存在し得るのだが...)ため、算術平均が使われることが多いようです。
sorted_data = data_open.sort_values() # あたいを並び替え
N = len(data_open)
if N%2==0:
median = (sorted_data[ int(N/2) ] + sorted_data[int(N/2) + 1]) / 2
else:
median = (sorted_data[int(N/2)])
print(median)1.16426pandasのDataFrameやnumpyではmedian()という関数で値を取得できます。
print(data_open.median())
print(np.median(data_open))1.16426
1.16426最頻値(mode)
最頻値(mode)はそのデータのなかで最も出現頻度の高い値です。基本的にカテゴリデータで使用されます。
今回の様な連続データの場合、それぞれのデータの絶対値が意味を持っているわけではありません。そのため、そのままの生データで最頻値を使うことはほぼないと言っていいと思います。
しかし、FXのデータからそれぞれの状況をラベルに変換した場合にはこれはカテゴリデータと言えるため最頻値を使う可能性は出てくるのでしょう。
例:USDJPYの最大買値が前日に比べてプラスの場合1、同じ値の場合0,マイナスの場合−1というデータにする。
from collections import Counter
counter = Counter(data_open)
print(counter.most_common()[0][0])1.17416一見それらしい値が出ても、意味がわかっていればこの計算にほとんど意味がないことがわかりますね。
まとめ
FXの生データそのままの代表値としては算術平均や中央値を使うのが良さそうですね。しかし、もしこの生のデータに他のデータ(各国の経済指標など)を組み合わせてある条件をみたすかどうかで場合わけ...のような場合には最頻値を使うことになるでしょう。
散らばりの指標
平均の様な値はあくまでそのデータがどのあたりの『位置』に存在するかという指標にしかなりません。そこでデータがどのあたりの範囲に存在するのかという指標として散らばりの推定をします。
散らばりの指標としては主に度数分布、箱ひげ図、分散、標準偏差などが用いられます。
度数分布(Frequency Distribution)
度数分布(Frequency Distribution)は値の出現頻度を数えた表のことを良い、それを棒グラフで表示したものをヒストグラムと言います。しかし、連続データをそのまま表示すると細かすぎるので、その場合にはデータを値ごとにクラス分けし、そのクラスの出現頻度を計測するのが良いでしょう。
いくつのクラスに分けるのか検討がつかないときにはスタージェスの公式(Sturges' rule)をつかってみましょう。この公式はN:全データ数からk:階級の数の目安をつける公式です。
k = log_2( N ) + 1
k : 階級の数
N : 全データ数まずはクラスごとにデータを分けて表示してみます。
from collections import Counter
RANK_NUM = int(np.log2(N)) + 1 # 階級数
counter = Counter(data_open)
classed_data = pd.cut(data_open, RANK_NUM,labels=False)
classed_data.plot()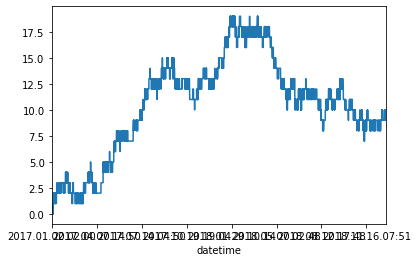
ヒストグラムの表示はpandasのDataSeriesのhist()メソッドで表示できます。
classed_data.hist()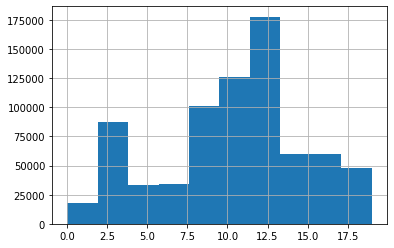
なるほど...なんとなくの分布はわかりますね。
ただ、これでひと目でデータの散らばりがわかると言うとそんなことはなさそうですね。
箱ひげ図(box-plot)
箱ひげ図(box-plot)とはデータを小さい順に並べて4分割したものを図にしたもので、データの散らばりを視覚的・直感的に理解することができます。
FXでよく使用するローソク足とは見た目が似ていますが全くの別物なので注意してください。
データは以下の様に図にされます。
- 0/4の点(最小値):下髭の下はしになる
- 1/4の点 :箱の底辺になる
- 2/4の点(中央値):箱の内部に線としてひかれる
- 3/4の点 :箱の上辺になる
- 4/4の点(最大値):上髭の上はしになる
pandasの場合DataFrameではbox_plot()メソッド、Seriesではplot.box()メソッドで箱ひげ図を表示できます。
data_open.plot.box()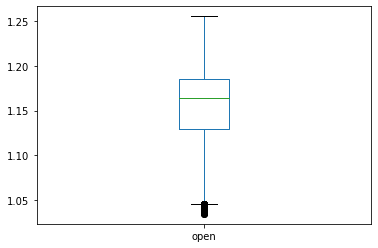
DataFrameで表示する際にはしっかり表示する行を選んでplotしましょう。DataFrameはloc[ {取得したい列},{取得したい行} ]で特定の行、列のデータのみを取得できます。
data_compare = data_concated.loc[:,['open','close','high','low']]
data_compare.boxplot()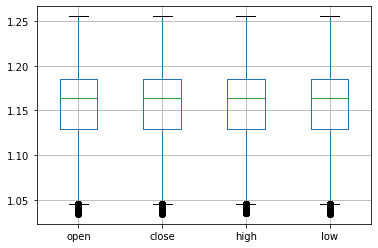
箱髭図をみると中の箱の高さが少し低く、上下とも髭が長いことがわかります。中間近くの出現頻度が多く、また変動も大きいデータであると言えます。
ここから値の散らばりを視覚的にではなく数値的に表現する平均絶対誤差、分散、標準偏差について解説します。
平均絶対偏差(mean absolute deviation, average absolute deviation)
平均絶対偏差(mean abxolute deviation, average absolute deviation)はデータの平均と各データとの差(偏差)の絶対値の平均です。
mean = data_open.mean()
mad = abs((data_open - mean)).sum()/data_open.size
print("平均絶対偏差:{}".format(mad))平均絶対偏差:0.04094061155634395分散(variance)
分散(variance)は偏差の2乗の平均です。実際のデータに分散の定義に当てはめ計算を標本分散(sample variance)と言います。
実際のデータで計算した標本分散は本当の分散より低く見積もってしまいます。このバイアスを修正するために標本分散 × ( n/( n-1 ) )をした値のことを不偏分散(unbiased variance)と言います。統計の推論で一般に分散というとこちらの不偏分散のことを言います。
nはデータ数です。
不偏分散を計算するために標本分散にかけている n/( n-1 )という値は下の様な関数です。
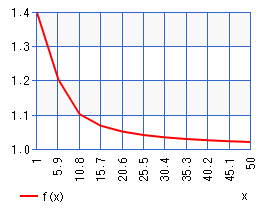
n/(n-1)はn:データ数が多くなるほど1に近づいています。つまり、標本分散から不偏分散への計算は
データ数がすくない : 大きく修正
データ数が膨大にある: ほとんど何もしない
な計算であるとも言えるでしょう。
では実際にそれぞれの計算をしていきます。
# データ数
N = data_open.size
# 平均を計算
mean = data_open.mean()
# すべての偏差の二乗を計算
deviation_2 = ( data_open - mean ) ** 2
# 標本標準偏差を計算
sv = deviation_2.sum() / N
# 不偏標準偏差を計算
uv = sv * N/(N-1)
print("標本分散:{}".format(sv))
print("不偏分散:{}".format(uv))標本分散:0.00265104848040972
不偏分散:0.0026510520424930777pandasのDataFrame、Seriesではvar()というメソッドで一発で取得できます。
print("標本分散:{}".format(data_open.var(ddof=0)))
print("不偏分散:{}".format(data_open.var(ddof=1)))標本分散:0.00265104848040972
不偏分散:0.0026510520424930777標準偏差(standard deviation)
標準偏差(standard deviation)は分散の平方根をとった値です。分散は値が2乗してあるため単位も2乗されてしまいます。
そのため元データと同じ尺度で議論できるこちらがよく使われます。
print("標準偏差:{}".format(uv**0.5))pandasのDataFrameには標準偏差を直接計算するstd()メソッドが用意されています。
print("標準偏差:{}".format(data_open.std()))-
2019年11月26日【初心者チュートリアル】Django2でブログ作成(Part14)〜ページのデザイン~Djangoは簡単にWebアプリケーションを作成できるフレームワークです。この記事は初心…
-
2019年11月5日【初心者チュートリアル】Django2でブログ作成(Part2)〜アプリケーションを作成〜Djangoは簡単にWebアプリケーションを作成できるフレームワークです。この記事は初心…
-
2019年11月14日【初心者チュートリアル】Django2でブログ作成(Part10)〜templateの作成~Djangoは簡単にWebアプリケーションを作成できるフレームワークです。この記事は初心…
-
2021年6月16日【Django】データベースのダンプファイル取り扱い方解説この記事ではDjangoコマンドを使ったダンプファイルの作成・読み込みの方法などについて…
-
2019年12月3日【Django2.2】QuerySetでクエリが実行されるタイミングについて解説Djangoでデータベースを操作する際に使うQuerySetは裏でSQLを発行しています…
-
2019年10月25日Python3.6でカラー画像をモノクロ・グレー画像にする方法解説この記事ではRGB画像をpython3.6のライブラリPillowを使ってグレーまたはモ…
The 10 Most Terrifying Things About UK Onlyfans Pornstars
uk onlyfans pornstars
Welcome to the world of adult Dating loveawake.ru